Mr Speaker

Bill Gates vs. Steve Jobs. Windows vs. Macintosh. After a decade of intense psychological duelling, a clear winner has emerged in the ultimate operating system battle: "Calculator Chicken"...

...One thing that computers can do fairly well is calculate. Give them two numbers - even really big ones like 383821 or 64342 or 128793 - and they can add them up fast. They can subtract, multiply or divide them really fast too. And it's easy for programmers to make them do it. It's like, one of the first programs you learn to make - a calculator. It was probably the first program made for Microsoft Windows, and probably the first program made for Apple Macintosh.

Computers have changed a lot since those calculators. Macs look all shmick and super cool, Windows looks like a shiny MacDonald's playground, and they certainly look a lot better than they did in 1990.

But do you want to know something weird - until recently they both contained the same calculator programs they'd had since the beginning of computer time. Check them out:

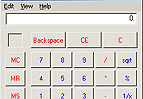
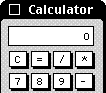
<-Old School Windows

         Old School Mac->

Now, here's the weird thing - when you make a program for Windows or Mac you generally don't get a say in what it looks like. If you want a button, you say "draw a button", and the operating system will draw you a button that looks like all the other buttons on all the other programs. This gives programs the "look and feel" of the operating system and means people don't have to figure out what a button is on every program they use.

Therefore, Windows and Mac haven't simply not upgraded their calculator programs, but purposely taken time and resources to make them look old. They have changed the look of every single program except for the easiest to change.

Why would they do that? Well, I'll tell you why. It's because Bill Gates and Steve Jobs were involved in a game of Calculator Chicken.

With every release, with every upgrade, every year - for over 10 years - each refused to dodge the on-coming train of "calculator redesign". A game of nerve and skill where the stakes were high. The winner would achieve infinite respect - the loser, an eternity of ridicule...

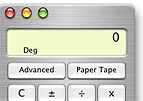...Recently I had a chance to use Mac's OSX and was shocked to see - Bill Gates has won calculator chicken. Steve had cracked. It must have been a torturing 10 years for him. But "the winner steals the glory, while the loser takes the pain".

I guess it makes sense. Windows looks like a barrel full of armpits - in fact, the Window's calculator program is probably the nicest looking app on my system.

So with everlasting victory to Microsoft I bet ya any money that Windows "Longhorn" has an all-new and improved calculator. But in my mind, simple maths will never be the same again.